13 Assembler Programming
In BASIC there are operators to perform multiplication, division, iteration etc., but in assembler the only operations provided are far more primitive and require a more thorough understanding of how the inside of the machine works. The ATOM is unique in that it enables BASIC and assembler to be mixed in one program. Thus the critical sections of programs, where speed is important, can be written in assembler, but the body of the program can be left in BASIC for simplicity and clarity.
The following table gives the main differences between BASIC and assembler:
| BASIC | Assembler |
| 26 variables | 3 registers |
| 4-byte precision | 1 byte precision |
| Slow – assignment takes over 1 msec. | Fast – assignments take 10 usec. |
| Multiply and divide | No multiply or divide |
| FOR...NEXT and DO...UNTIL loops | Loops must be set up by the programmer |
| Language independent of | Depends on instruction computer set of chip |
| Protection against overwriting program | No protection |
However, do not be discouraged; writing in assembler is rewarding and gives you a greater freedom and more ability to express the problem that you are trying to solve without the constraints imposed on you by the language. Remember that, after all, the BASIC interpreter itself was written in assembler.
A computer consists of three main parts:
1. The memoryIn the ATOM these parts are as follows:
1. Random Access Memory (RAM) and Read-Only Memory (ROM).When programming in BASIC it is not necessary to understand how these parts are working together, and how they are organised inside the computer. However in this section on assembler programming a thorough understanding of all these parts is needed.
The computer's memory can be thought of as a number of 'locations’, each capable of holding a value. In the unexpanded ATOM there are 2048 locations, each of which can hold one of 256 different values. Only 512 of these locations are free for you to use for programs; the remainder are used by the ATOM operating system, and for BASIC's variables.
_95_Somehow it must be possible to distinguish between one location and another. Houses in a town are distinguished by each having a unique address; even when the occupants of a house change, the address of the house remains the same. Similarly, each location in a computer has a unique 'address', consisting of a number. Thus the first few locations in memory have the addresses 0, 1, 2, 3...etc. Thus we can speak of the 'contents' of location 100, being the number stored in the location of that address.
Having been brought up counting in tens it seems natural for us to use a base of ten for our numbers, and any other system seems clumsy. We have just ten symbols, 0, 1, 2, ... 8, 9, and we can use these symbols to represent numbers as large as we please by making the value of the digit depend on its position in the number. Thus, in the number 171 the first '1' means 100, and the second '1' means 1. Moving a digit one place to the left increases its value by 10; this is why our system is called 'base ten' or 'decimal'.
It happens that base 10 is singularly unsuitable for working with computers; we choose instead base 16, or 'hexadecimal', and it will pay to spend a little time becoming familiar with this number system.
First of all, in base 16 we need 16 different symbols to represent the 16 different digits. For convenience we retain 0 to 9, and use the letters A to F to represent values of ten to fifteen:
Hexadecimal digit: 0 1 2 3 4 5 6 7 8 9 A B C D E F Decimal value: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
The second difference between base 16 and base 10 is the value accorded to the digit by virtue of its position. In base 16 moving a digit one place to the left multiplies its value by 16 (not 10).
Because it is not always clear whether a number is hexadecimal or decimal, hexadecimal numbers will be prefixed with a hash ’#' symbol. Now look at the following examples of hexadecimal numbers:
#B1
The 'B' has the value 11*16 because it is one position to the left of the units column, and there is 1 unit; the number therefore has the decimal value 176+1 or 177.
#123
The '1' is two places to the left, so it has value 16*16*1.
The '2' has the value 16*2. The '3' has the value 3. Adding these
together we obtain: 256+32+3 = 291.
There is really no need to learn how to convert between
hexadecimal and decimal because the ATOM can do it for you.
To print out the decimal value of a hexadecimal number, such as #123, type:
PRINT #123
The answer, 291, is printed out.
To print, in hexadecimal, the value of a decimal number, type:
_96_PRINT &123
The answer, #7B, is printed out. The '&' symbol means
'print in hexadecimal'. Thus writing:
PRINT {
will print 123.
We can now look at the contents of some memory, locations in the ATOM's memory. To do this we use the '?’ query operator, which means 'look in the following memory location'. The query is followed by the address of the memory location we want to examine. Thus:
PRINT ?#e1
will look at the location whose address is #El, and print out
its value, which will be 128 (the cursor flag). Try looking at
the contents of other memory locations; they will all contain
numbers between 0 and 255.
It is often convenient to look at several memory locations in a
row. For example, to list the contents of the 32 memory locations
from #80 upwards, type:
FOR N=0 TO 31; PRINT N?#80; NEXT N
The value of N is added to #80 to give the address of the location whose contents are printed out; this is repeated for each value of N from 0 to 31. Note that N?#80 is identical to ?(N+#80).
A word of caution: although it is quite safe to look at any memory location in the ATOM, care should be exercised when changing memory locations. The examples given here specify locations that are not used by the ATOM system; if you change other locations, be sure you know what you are doing or you may lose the stored text, or have to reset the ATOM with BREAK.
First print the contents of #80. The value there will be whatever was in the memory when you switched on, because the ATOM does not use this location. To change the contents of this location to 7, type:
?#80=7
To verify the change, type:
PRINT ?#80
Try setting the contents to other numbers. What happens if you try to set the contents of the location to a number greater than 255?
If locations can only hold numbers between 0 and 255, how is text stored in the computer's memory? The answer is that each number is used to represent a different character, and so text is simply a sequence of numbers in successive memory locations. There is no danger in representing both numbers and characters in the same way because the context will always make it clear how they should be interpreted.
To find the number corresponding to a character the CH function can be used. Type:
PRINT CH"A"
and the number 65 will be printed out. The character "A" is represented internally by the number 65. Try repeating this for B, C, D, E... etc. You will notice that there is a certain regularity. Try:
_97_PRINT CH"0"
and repeat for 1, 2, 3, 4...etc.
The size of each memory location is called a 'byte'. A byte can represent any one of 256 different values. A byte can hold a number between 0 and 255 in decimal, or from #00 to #FF in hexadecimal. Note that exactly two digits of a hex number can be held in one byte. Alternatively a byte can be interpreted as one of 256 different characters. Yet another option is for the byte to be interpreted as one of 256 different instructions for the processor to execute.
The main part of this chapter will deal with the ATOM's brain, the Central Processing Unit or CPU. In the ATOM this is a 6502, a processor designed in 1975 and the best-selling 8-bit microprocessor in 1979. Much of what you learn in this chapter is specific to the 6502, and other microprocessors will do things more or less differently. However, the 6502 is an extremely popular microprocessor with a modern instruction set, and a surprisingly wide range of addressing modes; furthermore it uses pipelining to give extremely fast execution times; as fast as some other microprocessors running at twice the speed.
The CPU is the active part of the computer; although many areas of memory may remain unchanged for hours on end when a computer is being used, the CPU is working all the time the machine is switched on, and data is being processed by it at the rate of 1 million times a second. The CPU's job is to read a sequence of instructions from memory and carry out the operations specified by those instructions.
The instructions to the CPU are again just values in memory locations, but this time they are interpreted by the CPU to represent the different operations it can perform, For example, the instruction #18 is interpreted to mean 'clear carry flag'; you will find out what that means in a moment. The first byte of all instructions is the operation code, or 'op code'. Some instructions consist of just the op code; other instructions specify data or an address in the bytes following the op code.
Many of the operations performed by the CPU involve a temporary location inside the CPU known as the accumulator, or A for short (nothing to do with BASIC's variable A). For example, to add two numbers together you actually have to load the first number into the accumulator from memory, add in the second number from memory, and then store the result somewhere. The following instructions will be needed:
| Mnemonic | Description | Symbol |
| LDA | Load accumulator with memory | A=M |
| STA | Store accumulator in memory | M=A |
| ADC | Add memory to accumulator with carry | A=A+M+C |
| We will also need one extra instruction: | ||
| CLC | Clear carry | C=0 |
The three letter names such as LDA and STA are called the instruction mnemonics; they are simply a more convenient way of representing the instruction than having to remember the actual op code, which is just a number.
_98_The ATOM automatically converts these mnemonics into the op codes. This process of converting mnemonics into codes is called 'assembling'. The assembler takes a list of mnemonics, called an assembler program, and converts them into 'machine code', the numbers that are actually going to be executed by the processor.
Enter the following assembler program:
10 DIM P(-1) 20[ 30 LDA #80 40 CLC 50 ADC #81 60 STA #82 70 RTS 80] 90 END
The meaning of each line in this assembler program is as follows:
| 10. | The DIM statement is not an assembler mnemonic; it just tells the assembler where to put the assembled machine code; at TOP in this case. |
| 20. | The '[' and ']’ symbols enclose the assembler statements. |
| 30. | Load the accumulator with the contents of the memory
location with address #80. (The contents of the memory location are not changed.) |
| 40. | Clear the carry flag. |
| 50. | Add the contents of location #81 to the accumulator,
with the carry. (Location #81 is not changed by this operation.) |
| 60. | Store the contents of the accumulator to location
#82. (The accumulator is not changed by this operation.) |
| 70. | The RTS instruction will usually be the last
instruction of any program; it causes a return to the ATOM BASIC system from the machine-code program. |
| 80. | See 20. |
| 90. | The END statement is not an assembler mnemonic; it just denotes the end of the text. |
Now type RUN and the assembler program will be assembled. An 'assembler listing' will be printed out to show the machine code that the assembler has generated to the left of the corresponding assembler mnemonics:
_99_RUN
20 824D 30 824D A5 80 LDA #80 40 824F 18 CLC 50 8250 65 81 ADC #81 60 8252 85 82 STA #82 70 8254 60 RTS ^ ^ ^ ^ ^ | | | | mnemonic statement | | | instruction data/address | | instruction op code | location counter statement line number
The program has been assembled in memory starting at #824D, immediately after the program text. This address may, be different when you do this example if you have inserted extra spaces into the program, but that will not affect what follows. All the numbers in the listing, except for the line numbers on the left, are in hexadecimal; thus #18 is the op code for the CLC instruction, and #A5 is the op code for LDA. The LDA instruction consists of two bytes; the first byte is the op code, and the second byte is the address; #80 in this case.
Typing RUN assembled the program and stored the machine code in memory directly after the assembler program. The address of the end of the program text is called TOP; type:
PRINT &TOP
and this value will be printed out in hexadecimal. It will correspond with the address opposite the first instruction, #A5. The machine code is thus stored in memory as follows:
A5 80 18 65 81 85 82 60 TOP
So far we have just assembled the program, generated the machine code, and put the machine code into memory.
To execute the machine-code program at TOP, type:
LINK TOP
What happens? Nothing much; we just return to the '>' prompt. But the program has been executed, although it only took 17 microseconds, and the contents of locations #80 and #81 have indeed been added together and the result placed in #82.
Execute it again, but first set up the contents of #80 and #81 by typing:
?#80=7; ?#81=9
If you wish you can also set the contents of #82 to 0. Now type:
LINK TOP
and then look at the contents of #82 by typing:
_100_PRINT ?#82
The result is 16 (in decimal); the computer has just added 7 and 9 and obtained 16!
Try executing the program for different numbers in #80 and #81. You might like to try the following:
?#80=140; ?#81=150 LINK TOP
What is the result?
The reason why the result is only 34, and not 290 as one might expect, is that the accumulator can only hold one byte. Performing the addition in hexadecimal:
Decimal Hexadecimal 140 8C +150 +96 290 122
Only two hex digits can fit in one byte, so the '1' of #122 is lost, and only the #22 is retained. Luckily the '1' carry is retained for us in, as you may have guessed, the carry flag. The carry flag is always set to the value of the carry out of the byte after an addition or subtraction operation.
The carry flag makes it a simple matter to add numbers as large as we please. Here we shall add two two-byte numbers to give a two-byte answer, although the method can be extended to any number of bytes. Modify the program already in memory by retyping lines 50 to 120, leaving out the lower-case comments, to give the following program:
10 DIM P(-1) 20[ 30 LDA #80 low byte of one number 40 CLC 50 ADC #82 low byte of other number 60 STA #84 low byte of result 70 LDA #81 high byte of one number 80 ADC #83 high byte of other number 90 STA #85 high byte of result 100 RTS 110] 120 END_101_Assemble the program: RUN20 826K 30 826E AS 80 LDA #80 40 8270 18 CLC 50 8271 65 82 ADC #82 60 8273 85 84 STA #84 70 8275 A5 81 LDA #81 80 8277 65 83 ADC #83 90 8279 85 85 STA #85 100 827B 60 RTS
Now set up the two numbers as follows:
?#80=#8C; ?#81=#00 ?#82=#96; ?#83=#00
Finally, execute the program:
LINK TOP
and look at the result, printing it in hexadecimal this time for convenience:
PRINT &?#84, &?#85
The low byte of the result is #22, as before using the one-byte addition program, but this time the high byte of the result, #1, has been correctly obtained. The carry generated by the first addition was added in to the second addition, giving:
0+0+carry = 1
Try some other two-byte additions using the new program.
The subtract instruction is just like the add instruction, except that there is a 'borrow’ if the carry flag is zero. Therefore to perform a single-byte subtraction the carry flag should first be set with the SEC instruction:
SBC Subtract memory from accumulator with borrow A=A-M-(1-C) SEC Set carry flag C=1
The ATOM contains routines for the basic operations of printing a character to the VDU, and reading a character from the keyboard, and these routines can be called from assembler programs. The addresses of these routines are standardised throughout the Acorn range of software, and are as follows:
Name Address Function OSWRCH OFFF4 Puts character in accumulator to output (VDU) OSRDCH 4FFE3 Read from input (keyboard) into accumulator
In each case all the other registers are preserved. The names of these routines are acronyms for 'Operating System WRite CHaracter' and 'Operating System ReaD CHaracter' respectively. These routines are executed with the following instruction:
JSR Jump to subroutine
A detailed description of how the JSR instruction works will be left until later.
The following program outputs the contents of memory location #80 as a character to the VDU, using a call to the subroutine OSWRCH:
_102_10 DIM P(-1) 20 W=#FFF4 30[ 40 LDA #80 50 JSR W 60 RTS 70] 80 END
The variable W is used for the address of the OSWRCH routine. Assemble the program, and then set the contents of 480 to #21:
?#80=#21
Then execute the program:
LINK TOP
and an exclamation mark will be printed out before returning to the ATOM's prompt character, because 021 is the code for an exclamation mark. Try executing the program with different values in #80.
In the previous example the instruction:
LDA #80
loaded the accumulator with the contents of location #80, which was then set to contain #21, the code for an exclamation mark. If at the time that the program was written it was known that an exclamation mark was to be printed it would be more convenient to specify this in the program as the actual data to be loaded into the accumulator. Fortunately an 'Immediate' addressing mode is provided which achieves just this. Change the instruction to:
LDA @#21
where the '@' (at) symbol specifies to the assembler that immediate addressing is required. Assemble the program again, and note that the instruction op-code for LDA @#21 is #A9, not #A5 as previously. The op-code of the instruction specifies to the CPU whether the following byte is to be the actual data loaded into the accumulator, or the address of the data to be loaded.
_104_All the assembler programs in the previous section have been executed instruction by instruction following the sequence specified by the order of the instructions in memory. The jump and branch instructions enable' the flow of control to be altered, making it possible to implement loops.
The JMP instruction is followed by the address of the instruction to be executed next.
JMP Jump
Before using the JMP instruction we need to be able to indicate to the assembler where we want to jump to, and to do this conveniently 'labels' are needed. In the assembler labels are variables of the form AA to ZZ followed by a number (0, 1, 2 ... etc). If you are already familiar with ATOM BASIC you will recognise these as the arrays.
First the labels to be used in an assembler program must be declared in the DIM statement. Note that we still need to declare P(-1) as before, and this must be the last thing declared. For example, to provide space for four labels LL0, LL1, LL2, and LL3 we would declare:
DIM LL(3), P(-1)
Labels used in a program are prefixed by a colon ':' character. For example, enter the following assembler program:
10 DIM LL(3),P(-1) 20 W=#FFF4 30[ 40:LL0 LDA @#2A 50:LL1 JSR W 60 JMP LL0 70] 80 END
To execute the program the procedure is slightly different from the previous examples, because space has now been assigned at TOP for the labels. When using labels in an assembler program you should place a label at the start of the program, as with LLO in this example, and LINK to that label. So, in this example, execute the program with:
LINK LL0
The program will output an asterisk, and then jump back to the
previous instruction. The program has become stuck in an endless
loop! If you know BASIC, compare this program with the BASIC
program in section 4.6 that has the same effect.
A flowchart for this program is as follows:
Try pressing ESCAPE. ESCAPE will not work; it only works in BASIC programs, and here we are executing machine code instructions so ESCAPE is no longer checked for. Fortunately there is one means of salvation: press BREAK, and then type OLD to retrieve the original program.
The carry flag has already been introduced; it is set or cleared as the result of an ADC instruction. The CPU contains several other flags, which are set or cleared depending on the outcome of certain instructions; this section will introduce another one.
The zero flag, called Z, is set if the result of the previous operation gave zero, and is cleared otherwise. So, for example:
LDA #80
would set the zero flag if the contents of #80 were zero.
The conditional branches enable the program to act on the outcome of an operation. The branch instructions look at a specified flag, and then either carry on execution if the test was false, or cause a branch to a different address if the test was true. There are 8 different branch instructions, four of which will be introduced here:
BEQ Branch if equal to zero (i.e. Z=1) BNE Branch if not equal to zero (i.e. Z=0) BCC Branch if carry-flag clear (i.e. C=0) BCS Branch if carry-flag set (i.e. C=1)
The difference between a 'branch' and a 'jump' is that the jump instruction is three bytes long (op-code and two-byte address) whereas the branch instructions are only two bytes long (op-code and one-byte offset). The difference is automatically looked after by the assembler.
The following simple program will print an exclamation mark if #80 contains zero, and a star if it does not contain zero; the comments in lower-case can be omitted when you enter the program:
_106_10 DIM BB(3),P(-1) 20 W=#FFF4 30[ 40:BBO LDA #80 50 BEQ BB1 if zero go to BB1 60 LDA @#2A star 70 JSR W print it BO RTS return 90:BB1 LDA @#21 exclamation mark 100 JSR W print it 110 RTS return 120] 130 END
A flowchart for this program is as follows:
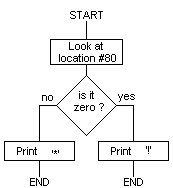
Now assemble the program with RUN as usual. You will almost certainly get the message:
OUT OF RANGE:
before the line containing the instruction BEQ BB1, and the offset in the branch instruction will have been set to zero. The message is produced because the label BB1 has not yet been met when the branch instruction referring to it is being assembled; in other words, the assembler program contains a forward reference. Therefore you should assemble the program a second time by typing RUN again. This time the message will not be produced and the correct offset will be calculated for the branch instruction.
Note that whenever a program contains forward references it should be assembled twice before executing the machine code.
Now execute the program by typing:
LINK BB0
for different values in #80, and verify that the behaviour is as specified above.
The CPU contains two registers in addition to the accumulator, and these are called the X and Y registers. As with the accumulator, there are instructions to load and store the X and Y registers:
LDX Load X register from memory X=M LDY Load Y register from memory Y=M STX Store X register to memory M=X STY Store Y register to memory M=Y
However the X and Y registers cannot be used as one of the operands in arithmetic or logical instructions like the accumulator; they have their own special uses, including loop control and indexed addressing.
_107_The X and Y registers are particularly useful as the control variables in iterative loops, because of four special instructions which will either increment (add 1 to) or decrement (subtract 1 from) their values:
INX Increment X register X=X+1 INY Increment Y register Y=Y+1 DEX Decrement X register X=X-1 DEY Decrement Y register Y=Y-1
Note that these instructions do not affect the carry flag, so incrementing #FF will give #00 without changing the carry bit. The zero flag is, however, affected by these instructions, and the following program tests the zero flag to detect when X reaches zero.
The iterative loop enables the same set of instructions to be executed a fixed number of times. For example, enter the following program:
10 DIM LL(4),P(-1) 20 W=#FFF4 30[ 40:LL0 LDX @8 initialise X 50:LL1 LDA @#2A code for star 60:LL2 JSR W output it 70 DEX count it 80 BNE LL2 all done? 90 RTS 100 ] 110 END
A flowchart for the program is as follows:
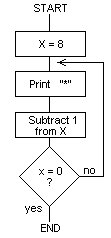 _108_
_108_
Assemble the program by typing RUN. This program prints out a star, decrements the X register, and then branches back if the result after decrementing the X register is not zero. Consider what value X will have on successive times around the loop and predict how many stars will be printed out; then execute the program with LINK LLO and see if your prediction was correct. If you were wrong, try thinking about the case where X was initially set to 1 instead of 8 in line 40.
How many stars are printed if you change the instruction on line 40 to LDX @0 ?
In the previous example the condition X=0 was used to terminate the loop. Sometimes we might want to count up from 0 and terminate on some specified value other than zero. The compare instruction can be used to compare the contents of a register with a value in memory; if the two are the same, the zero flag will be set. If they are not the same, the zero flag will be cleared. The compare instruction also affects the carry flag.
CMP Compare accumulator with memory A-M CPX Compare X register with memory X-M CPY Compare Y register with memory Y-M
Note that the compare instruction does not affect its two operands; it just changes the flags as a result of the comparison.
The next example again prints 8 stars, but this time it uses X as a counter to count upwards from 0 to 8:
10 DIM LL(2),P(-1) 20 W=#FFF4 30[ 40:LL0 LDX @0 start at zero 50:LL1 LDA @#2A code for star 60 JSR W output it 70 INX next X 80 CPX @8 all done? 90 BNE LL1 100 RTS return 110] 120 END
In this program X takes the values 0, 1, 2, 3, 4, 5, 6, and 7. The last time around the loop X is incremented to 8, and the loop terminates. Try drawing a flowchart for this program.
In the previous two examples X was simply used as a counter, and so it made no difference whether we counted up or down. However, it is often useful to use the value of the control variable in the program. For example, we could print out the character in the X register each time around the loop. We therefore need a way of transferring the value in the X register to the accumulator so that it can be printed out by the OSWRCH routine. One way would be to execute:
STX #82 LDA #82
where #82 is not being used for any other purpose. There is a more convenient way, using one of four new instructions:
_109_TAX Transfer accumulator to X register X=A TAY Transfer accumulator to Y register Y=A TXA Transfer X register to accumulator A=X TYA Transfer Y register to accumulator A=Y
Note that the transfer instructions only affect the register
being transferred to.
The following example prints out the alphabet by making X cover
the range #41, the code for A, to #5A, the code for Z.
10 DIM LL(2),P(-1) 20 W=#FFF4 30[ 40:LL0 LDX @#41 start at A 50:LL1 TXA put it in A 60 JSR W print it 70 INX next one 80 CPX @#5B done Z? 90 BNE LL1 if so – continue 100 RTS else – return 110] 120 END
Modify the program to print the alphabet in reverse order, Z to A.
All these examples could have used Y as the control variable instead of X in exactly the same way.
_110_So far we have considered each memory location, or memory byte, as being capable of holding one of 256 different numbers (0 to 255), or one of 256 different characters. In this section we examine an alternative representation, which is closer to the way a byte of information is actually stored in the computer's memory.
The computer memory consists of electronic circuits that can be put into one of two different states. Such circuits are called bistables because they have two stable states, or flip/flops, for similar reasons. The two states are normally represented as 0 and 1, but they are often referred to by different terms as listed below:

When the digits 0 and 1 are used to refer to the states of a bistable they are referred to as 'binary digits', or 'bits' for brevity.
With two bits you can represent four different states which can be listed as follows, if the bits are called A and B:
A: B: 0 0 0 1 1 0 1 1
With four bits you can represent one of 16 different values, since 2x2x2x2=16, and so each hexadecimal digit can be represented by a four-bit binary number. The hexadecimal digits, and their binary equivalents, are shown in the following table:
_111_
Decimal: Hexadecimal: Binary: 0 0 0 0 0 0 1 1 0 0 0 1 2 2 0 0 1 0 3 3 0 0 1 1 4 4 0 1 0 0 5 5 0 1 0 1 6 6 0 1 1 0 7 7 0 1 1 1 8 8 1 0 0 0 9 9 1 0 0 1 10 A 1 0 1 0 11 B 1 0 1 1 12 C 1 1 0 0 13 D 1 1 0 1 14 E 1 1 1 0 15 F 1 1 1 1
Any decimal number can be converted into its binary representation by the simple procedure of converting each hexadecimal digit into the corresponding four bits. For example:
Decimal: 25 Hexadecimal: 19 Binary: 0001 1001
Thus the binary equivalent of #19 is 00011001 (or, leaving out the leading zeros, 11001).
Verify the following facts about binary numbers:
1. Shifting a binary number left, and inserting a zero after it,
is the same as multiplying its value by 2.
e.g. 7 is 111 and 14 is 1110.
2. Shifting a binary number right, removing the last digit,
is the same as dividing it by 2 and ignoring the remainder.
We have already seen that we need exactly two hexadecimal digits to represent all the different possible values in a byte of information. It should now be clear that a byte corresponds to eight bits of information, since each hex digit requires four bits to specify it. The bits in a byte are usually numbered, for convenience, as follows:
7 6 5 4 3 2 1 0 0 0 0 1 1 0 0 1
Bit 0 is often referred to as the 'low-order bit’ or 'least-significant bit', and bit 7 as the 'high-order bit' or 'most-significant bit'. Note that bit 0 corresponds to the units column, and moving a bit one place to the left in a number multiplies its value by 2.
Many operations in the computer's instruction set are easiest to think of as operations between two bytes represented as two 8-bit numbers. This section examines three operations called 'logical' operations which are performed between the individual bits of the two operands. One of the operands is always the accumulator, and the other is a memory location.
_112_AND AND accumulator with memory A=A&M
The AND operation sets the bit of the result to a 1 only if the bit of one operand is a 1 AND the corresponding bit of the other operand is a 1. Otherwise the bit in the result is a zero. For example:
Hexadecimal: Binary: A9 1 0 1 0 1 0 0 1 E5 1 1 1 0 0 1 0 1 -- --------------- Al 1 0 1 0 0 0 0 1
One way of thinking of the AND operation is that one operand acts as a 'mask', and only where there are ones in the mask do the corresponding bits in the other operand 'show through'; otherwise, the bits are zero.
ORA OR accumulator with memory A=A\M
The OR operation sets the bit of the result to a 1 if the corresponding bit of one operand is a 1 OR the corresponding bit of the other operand is a 1, or indeed, if they are both ones; otherwise the bit in the result is zero. For example:
Hexadecimal: Binary: A9 1 0 1 0 1 0 0 1 E5 1 1 1 0 0 1 0 1 -- --------------- ED 1 1 1 0 1 1 0 1
EOR Exclusive-OR accumulator with memory A=A:M
The exclusive-OR operation is like the OR operation, except that the corresponding bit in the result is 1 only if the corresponding bit of one operand is a 1, or if the corresponding bit of the other operand is a 1, but not if they are both ones. For example:
Hexadecimal: Binary: A9 1 0 1 0 1 0 0 1 E5 1 1 1 0 0 1 0 1 -- --------------- 4C 0 1 0 0 1 1 0 0
Another way of thinking of the exclusive-OR operation is that the bits of one operand are inverted where the other operand has ones.
Music is composed of vibrations of different frequencies that stimulate our ears to give the sensations of tones and noise. A single tone is a signal with a constant rate of vibration, and the 'pitch' of the tone depends on the frequency of the vibration: the faster the vibration, or the higher the frequency of vibration, the higher is the perceived pitch of the tone. The human ear is sensitive to frequencies from about 10 Hz (10 vibrations per second) up to about 16 kHz (16,000 vibrations a second). Since the ATOM can execute up to 500000 instructions per second in machine code, it is possible to generate tones covering the whole audible range.
_113_The ATOM contains a loudspeaker which is controlled by an output line. The loudspeaker is connected to bit 2 of the output port whose address is #B002:
7 6 5 4 3 2 1 0 V + -- -- -> Speaker
To make the loudspeaker vibrate we can exclusive-OR the location corresponding to the output port with the binary number 00000100 so that bit 2 is changed each time. To make the ATOM generate a tone of a particular frequency we need to make the output driving the loudspeaker vibrate with the required frequency. Try the following program:
10 DIM VV(4),P(-1) 20 L=#B002 30[ 40:VV0 LDA L 50:VV1 LDX #80 60:VV2 DEX 70 BNE VV2 80 EOR @4 90 STA L 100 JMP VV1 ll0] 120 END
The immediate operand 4 in line 80 corresponds to the binary number 00000100. The program generates a continuous tone, and can only be stopped by pressing BREAK. (To get the program back after pressing BREAK, type OLD.) The inner loop, lines 60 and 70, gives a delay depending on the contents of #80; the greater the contents of #80, the longer the delay, and the lower the pitch of the tone in the loudspeaker.
To make the program generate a tone pulse, or a bleep, of a fixed length, we need another counter to count the number of iterations around the loop, and to stop the program when a certain number of iterations have been performed. The following program is based on the previous example, but contains an extra loop to count the number of cycles. The only lines you need to enter are 45, 95, 100, and 105:
_114_5 REM Bleep 10 DIM VV(4); P(-l) 20 L=#B002 30[ 40:VV0 LDA L 45 LDY #81 50:VV1 LDX #80 60:VV2 DEX 70 BNE VV2 80 EOR @4 90 STA L 95 DEY 100 BNE VV1 105 RTS 110] 120 END
Now the program generates a tone pulse whose frequency is determined by the contents of #80, and whose length is determined by #81.
To illustrate the operation of this program, the following BASIC program calls it, running through tones of every frequency it can generate:
200 ?#81=255 210 FOR N=1 TO 256 220 ?#80=N 230 LINK VV0 240 NEXT N 250 END
This program should be entered into memory with the previous example, and the END statement at line 120 should be deleted so that the BASIC program will execute the assembled Bleep program.
Try changing the statement on line 220 to:
220 ?#80=RND
to give something reminiscent of certain modern music!
One disadvantage of this program, which you may have noticed, is that the length of the bleep gets progressively shorter as the frequency of the note gets higher; this is because the program generates a fixed number of cycles of the tone, so the higher the frequency, the less time these cycles will take. To give bleeps of the same duration it is necessary to make the contents of #81 the inverse of #80. For an illustration of how to achieve this, see the Harpsichord program of section 17.2.
The rotate and shift operations move the bits in a byte either left or right. The ASL instruction moves all the bits one place to the left; what was the high-order bit is put into the carry flag, and a zero bit is put into the low-order bit of the byte. The ROL instruction is identical except that the previous value of the carry flag, rather than zero, is put into the low-order bit.
The right shift and rotate right instructions are identical, except that the bits are shifted to the, right:
ASL Arithmetic shift left one bit (memory or accumulator)
C <-- 7 6 5 4 3 2 1 0 <-- 0
LSR Logical shift right one bit (memory or accumulator)
_115_
0 --> 7 6 5 4 3 2 1 0 --> C
ROL Rotate left one bit (memory or accumulator)
+ -- 7 6 5 4 3 2 1 0 <-- C + -- -- -- -- -- -- -- -- -- --- +
ROR Rotate right one bit (memory or accumulator)
C --> 7 6 5 4 3 2 1 0 --+ + --- -- -- -- -- -- -- -- -- --+
It may seem surprising.that a computer, which follows an absolutely determined sequence of operations, can generate noise which sounds completely random. The following program does just that; it generates a pseudo-random sequence of pulses that does not repeat until 8388607 have been generated. As it stands the noise it generates contains components up to 27kHz, well beyond the range of hearing, and it takes over 5 minutes before the sequence repeats.
The following noise program simulates, by means of the shift and rotate instructions, a 23-bit shift register whose lowest-order input is the exclusive-OR of bits 23 and 18:
10 REM Random Noise 20 DIM L(2),NN(1),P(-1) 30 C=#B002 40[ 50:NN0 LDA L; STA C 60 AND @#48; ADC @#38 70 ASL A; ASL A 80 ROL L+2; ROL L+1; ROL L 90 JMP NN0 100] 110 LINK NN0
Incidentally, the noise generated by this program is an excellent signal for testing high-fidelity audio equipment. The noise should be reproduced through the system and listened to at the output. The noise should sound evenly distributed over all frequencies, with no particular peak at any frequency revealing a peak in the spectrum, or any holes in the noise revealing the presence of dips in the spectrum.
_116_So far the X and Y registers have simply been used as counters, but their most important use is in 'indexed addressing'. We have already met two different addressing modes: absolute addressing, as in:
LDA U
where the instruction loads the accumulator with the contents of location U, and immediate addressing as in:
LDA @#21
where the instruction loads the accumulator with the actual value #21.
In indexed addressing one of the index registers, X or Y, is used as an offset which is added to the address specified in the instruction to give the actual address of the data. For example, we can write:
LDA S,X
If X contains zero this instruction will behave just like LDA S. However, if X contains 1 it will load the accumulator with the contents of 'one location further on from S'. In other words it will behave like LDA S+1. Since X can contain any value from 0 to 255, the instruction LDA S,X gives you access to 256 different memory locations. If you are familiar with BASIC's byte vectors you can think of S as the base of a vector, and of X as containing the subscript.
The following program uses indexed addressing to print out a string of characters inverted. Recall that a string is held as a sequence of character codes terminated by a #D byte:
10 DIM LL(2),S(64),P(-1) 20 W=#FFF4 30[ 40:LL0 LDX @0 50:LL1 LDA S,X 60 CMP @#D 70 BEQ LL2 80 ORA @#20 90 JSR W 100 INX 110 BNE LL1 120:LL2 RTS 130] 140 END
Assemble the program by typing RUN twice, and then try the program by entering:
_117_$S="TEST STRING"LINK LL0
Another useful operation that can easily be performed in a machine-code routine is to look up a character in a string, and return its position in that string. The following subroutine reads in a character, using a call to the OSRDCH read-character routines, and saves in ?F the position of the first occurrence of that character in $T.
1 REM Index Routine 10 DIM RR(3),T(25),F(0),P(-1) 20 R=#FFE3; $T="ABCDEFGH" 30[ 160\Look up A in T 165:RR1 STX F; RTS 180:RR0 JSR R; LDX @LEN(T)-1 190:RR2 CMP T,X; BEQ RR1 210 DEX; BPL RR2; BMI RR0 220] 230 END
The routine is entered at RR0, and as it stands it looks for one of the letters A to H.
The following sections summarise all the addressing modes that are available on the 6502.
When the data for an instruction is known at the time that the program being written, immediate addressing can be used. In immediate addressing the second byte of the instruction contains the actual 8-bit data to be used by the instruction.
The '@' symbol denotes an immediate operand.
LDA @7 A9 07 V A: 07
Absolute addressing is used when the effective address, to be used by the instruction, is known at the time the program is being written. In absolute addressing the two bytes following the op-code contain the 16-bit effective address to be used by the instruction.
_118_
Data: LDA #3010,X AD 10 31 #3010: 34 V A: 34 Examples: LDA K SBC #3010
Zero page addressing is like absolute addressing in that the instruction specifies the effective address to be used by the instruction, but only the lower byte of the address is specified in the instruction. The upper byte of the address is assumed to be zero, so only addresses in page zero, from #0000 to #00FF, can be addressed. The assembler will automatically produce zero-page instructions when possible.
Data: LDA #80 A5 80 #0080: 34 V A: 34 Examples: BIT #80 ASL #9A
Indexed addressing is used to access a table of memory locations by specifying them in terms of an offset from a base address. The base address is known at the time that the program is written; the offset, which is provided in one of the index registers, can be calculated by the program.
In all indexed addressing modes one of the 8-bit index registers, X and Y, is used in a calculation of the effective address to be used by the instruction. Five different indexed addressing modes are available, and are listed in the following section.
The simplest indexed addressing mode is absolute indexed addressing. In this mode the two bytes following the instruction specify a 16-bit address which is to be added to one of the index registers to form the effective address to be used by the instruction:
_119_
LDA #3120,X BD 20 31 Data: + = #3132: 78 X: 12 V A: 78 Examples: LDA M,X LDX J,Y INC N,X
In zero,X indexed addressing the second byte of the instruction specifies an 8-bit address which is added to the X-register to give a zero-page address to be used by the instruction.
Note that in the case of the LDX instruction a zero,Y addressing mode is provided instead of the zero,X mode.
LDA #80,X B6 80 Data: + = #0082: 78 X: 12 V A: 78
Examples: LSR #80,X LDX #82,Y
It is sometimes necessary to use an address which is actually
computed when the program runs, rather than being an offset from
a base address or a constant address. In this case indirect
addressing is used.
The indirect mode of addressing is available for the JMP
instruction. Thus control can be transferred to an address
calculated at the time that the program is run.
Examples: JMP (#2800) JMP (#80)
For the dual-operand instructions ADC, AND, CMP, EOR, LDA, ORA, SEC, and STA, two different modes of indirect addressing are provided: pre-indexed indirect, and post-indexed indirect. Pure indirect addressing can be obtained, using either mode, by first setting the respective index register to zero.
_120_This mode of addressing is used when a table of effective addresses is provided in page zero; the X index register is used as a pointer to select one of these addresses from the table.
In pre-indexed indirect addressing the second byte of the instruction is added to the X register to give an address in page zero. The two bytes at this page zero address are then used as the effective address for the instruction.
LDA (#70,X) A1 70 Data: + = #0075: 23 30 #3023: AC X: 05 V A: AC Examples: STA (J,X) EOR (#60,X)
This indexed addressing mode is like the absolute,X or absolute,Y indexed addressing modes, except that in this case the base address of the table is provided in page zero, rather than in the bytes following the instruction. The second byte of the instruction specifies the page-zero base address.
In post-indexed indirect addressinq the second byte of the instruction specifies a page zero address. The two bytes at this address are added to the Y index register to give a 16-bit address which is then used as the effective address for the instruction.
_121_
LDA (#70),Y A1 70 #0070: 43 35 Data: += #3553: 23 Y: 10 V A: 23 Examples: CMP (J),Y ADC (066),Y
This section gives a short description of all the 6502's registers:
Accumulator – A
8-bit general-purpose register, which forms one operand in all the arithmetic and logical instructions.
Index Register – X
8-bit register used as the offset in indexed and pre-indexed indirect addressing modes, or as a counter.
Index Register – Y
8-bit register used as the offset in indexed and post-indexed indirect addressing modes.
Status Register – S
8-bit register containing status flags and interrupt mask:
Bit 0 Carry flag (C) Set if a carry occurs during an add operation;
cleared if a borrow occurs during a subtract operation;
used as a ninth bit in the shift and rotate instructions.1 Zero flag (Z) Set if the result of an operation is zero; cleared otherwise. 2 Interrupt disable (I) If set, disables the effect of the IRQ interrupt.
Is set by the processor during interrupts.3 Decimal mode flag (0) If set, the add and subtract operations work
in binary-coded-decimal arithmetic;
if clear, the add and subtract operations work
in binary arithmetic.4 Break command (B) Set by the processor during a BRK interrupt; otherwise cleared. 5 Unused 6 Overflow flag (V) Set if a carry occurred from bit 6 during an add operation;
cleared if a borrow occurred to bit 6 in a subtract operation.7 Negative flag (N) Set if bit 7 of the result of an operation is set; otherwise cleared.
Stack Pointer – SP
8-bit register which forms the lower byte of the address of the next free stack location; the upper byte of this address is always #01.
Program Counter – PC
16-bit register which always contains the address of the next instruction to be fetched by the processor.
_122_Machine-code subroutines written using the mnemonic assembler can be incorporated into BASIC programs, and several examples are given in the following sections.
The following machine-code routine, 'Replace’, can be used to perform a character-by-character substitution on a string. It assumes the existence of three strings called R, S, and T. The routine looks up each character of R to see if it occurs in string S and, if so, it is replaced with the character in the corresponding position in string T,
For example, if:
$S="TMP"; $T="SNF"
then the sequence:
$R="COMPUTER" LINK RR0
will change $R to "CONFUSER".
10 REM Replace 20 DIM LL(4),R(20),S(20),T(20) 40 FOR N=l TO 2; DIM P(-1) 50[ 60:LL0 LDX @0 70:LL1 LDY @0; LDA R,X _123_ 80 CMP @#D; BNE LL3; RTS finished 90:LL2 INY 100:LL3 LDA S,Y 110 CMP @#D; BEQ LL4 120 CMP R,X; BNE LL2 130 LDA T,Y; STA R,X replace char 140:LL4 INX; JMP LL1 next char 150] 160 NEXT N 200 END
The routine has many uses, including code-conversion, encryption and decryption, and character rearrangement.
To illustrate one application of the Replace routine, the following program converts any number from Arabic to Roman numerals:
10 REM Roman Numerals 20 DIM LL(4),Q(50) 30 DIM R(20),S(20),T(20) 40 FOR N=l TO 2; DIM P(-1) 50[ 60:LL0 LDX @0 70:LL1 LDY @0; LDA R,X 80 CMP @#D; BNE LL3; RTS finished 90:LL2 INY 100:LL3 LDA S,Y 110 CMP @#D; BEQ LL4 120 CMP R,X; BNE LL2 130 LDA T,Y; STA R,X replace char 140:LL4 INX; JMP LL1 next char 150] 160 NEXT N 200 $S="IVXLCDM"; $T="XLCDM??" 210 $Q=""; $Q+5="I"; $Q+10="ii" 220 $Q+15="iii"; $Q+20="iv"; $9+25="V" 230 $Q+30="vi"; $Q+35="vii" 240 Sq+40="viii"; $Q+45="ix" 250 DO $R="";D=10000 255 INPUT A 260 DO LINK LL0 270 $R+LEN(R)=$(Q+A/D*5) 280 A=A%D; D=D/10; UNTIL D=O 290 PRINT $R; UNTIL 0 Description of Program: Allocate labels and strings 40-160 Assemble Replace routine. 200 Set up strings of Roman digits 210-240 Set up strings of numerals for 0 to 9. 255 Input number for conversion 260 Multiply the Roman string R by ten by performing a character substitution. 270 Append string for Roman representation for A/D to end of R. 280 Look at next digit of Arabic number. 290 Print Roman string, and carry on. Variables: A – Number for conversion D – Divisor for powers of ten. LL(0..4) – Labels for assembler routine. LL0 – Entry point for Replace routine. N – Counter for two-pass assembly. P – Location counter. Q – $(Q+5*x) is string for Roman numeral X. $R – String containing Roman representation of A. $S – Source string for replacement. $T – Target string for replacement. Program size: 579 bytes.
The following program simulates a harpsichord; it uses the central section of the ATOM's keyboard as a harpsichord keyboard, with the keys assigned as follows:
E R Y U I P @ A S D F G H J K L ; [ ] E R Y U I P @
A S D F G H J K L ; [ ]
where the S key corresponds to middle C. The space bar gives a 'rest', and no other key on the keyboard has any effect.
_124_The tune is displayed on a musical stave as it is played, with the black notes designated as sharps. Pressing RETURN will then play the music back, again displaying it as it is played.
The program uses the Index routine, described in Section 16.3, to look up the key pressed, and a version of the Bleep routine in Section 15.4.1.
1 REM Harpsichord 10 DIM S(23),T(26),F(0) 15 DIM WW(2),RR(2),Z(128) 20 DIM P(-1) 30 PRINT $21 100[\generate NOTE 110:WW0 STA F; LDA @0 120:WW2 LDX F 130:WW1 DEX; NOP; NOP; BNE WW1 140 EOR @4; STA #B002 150 DEY; BNE WW2; RTS 160\READ KEY & LOOK UP IN T 165:RR1 STX F; RTS 170:RR0 JSR #FFE3 180 LDX @25 190:RR2 CMP T,X; BEQ RR1 210 DEX; BPL RR2; BMI RR0 220] 230 PRINT $6 380 X=#8000 390 D=256*#22 393 S!20=#01016572 395 S!16=#018898AB 400 S!12=#01CBE401 410 S!8=#5A606B79 420 S!4=#8090A1B5 430 S!0=#C0D7F2FF 450 $T="ASDFGHJKL;[]?ER?YUI?P@? ?" 460 T?24=#1B; REM ESCAPE 470 CLEAR 0 480 DO K=32 500 FOR M=0 TO 127; LINK RR0 505 IF ?F<>25 GOTO 520 508 IF M<>0 Q=m 510 K=128; GOTO 540 520 Z?M=?F 530 GOSUB d 540 NEXT M 780 K=32 800 FOR M=0 TO Q-1; WAIT; WAIT 810 ?F=Z?M; GOSUB d 820 NEXT M 825 UNTIL 0 830dREM DRAW TUNE 840 IF K<31 GOTO e 850 CLEAR 0 860 FOR N=34 TO 10 STEP -6 870 MOVE 0,N; DRAW 63,N 880 NEXT N 890 K=0 900eIF ?F=23 GOTO s 910 IF ?F>11 K?(X+32*(27-?F))=35; K=K+1 920 K?(X+32*(15-?F%12))=15 _125_ 930 K=K+1 960 A=S?(?F); Y=D/A 970 LINK WWO 980 RETURN 990sFOR N=0 TO 500;NEXT N 995 K=K+1; RETURN Description of Program: 100-150 Assemble bleep routine 160-210 Assemble index routine 393-430 Set up note values 450-460 Set up keyboard table 480-825 Main program loop 500-540 Play up to 128 notes, storing and displaying them. 800-820 Play back tune 830 d: Draw note on staves and play note 840-880 If first note of screen, draw staves 900-920 Plot note on screen 960-970 Play note 990-995 Wait for a rest Variables: A – Note frequency D – Duration count ?F – Key Index K – Column count on screen M – Counter N – Counter P – Location counter Q – Number of notes entered RR(0..2) – Labels in index routine RR0 – Entry point to read routine S?0..S?23 – Vector of note periods T?0..T?26 – Vector of keys corresponding to vector S WW(0..2) – Labels in note routine WW0 – Entry point to note routine X – Screen address Y – Number of cycles of note to be generated Z(0..128) – Array to store tune. Program size: 1049 bytes Extra storage: 205 bytes Machine code: 41 bytes Total size: 1295 bytes
Bulls and Cows is a game of logical deduction which has become very popular in the plastic peg version marketed as 'Mastermind'. In this version of the game the human player and the computer each think of a 'code', consisting of a string of four digits, and they then take turns in trying to guess the other player's code. A player is given the following information about his guess:
The number of Bulls – i.e. digits correct and in the right position. The number of Cows – i.e. digits correct but in the wrong position.
Note that each digit can only contribute to one Bull or one
Cow. The human player specifies the computer's score as two
digits, Bulls followed by Cows. For example, if the code string
were '1234' the score for guesses of '0004’, '4000', and
'4231' would be '10’, '01', and '22' respectively.
The following program plays Bulls and Cows, and it uses a
combination of BASIC statements to perform the main input and
output operations, and assembler routines to speed up sections of
the program that are executed very frequently; without them the
program would take several minutes to make each guess.
10 REM Bulls & Cows
20 DIM M(3),N(3),C(0),B(0),L(9)
23 DIM GG(10),RR(10)
25 DIM LL(10)
50 GOSUB z; REM Assemble code
60 GOSUB z; REM Pass Two
10OO REM MASTERMIND *****
1005 Y=1; Z=1
1007 @=2
1010 GOSUB c
1015 G=!M ;REM MY NUMBER
1020 GOSUB c; Q=!m
1030 I=0
1040 DO I=I+1
1050 PRINT "(" I ")" '
1100 IF Y GOSUB a
1150 IF Z GOSUB b
1350 UNTIL Y=0 AND Z=0
1400 PRINT "END"; END
1999***********************************
2000 REM Find Possible Guess
2010fGOSUB c; F=!M
2160wLINK LL7
2165 IF !M=F PRINT "YOU CHEATED"; END
2170 X=1
2180v!N=GG(X)
2190 LINK LL2
2200 IF !C&#FFF<>RR(X) THEN GOTO w
2210 IF X<I THEN X=X+1; GOTO v
2220 Q=!m; RETURN
3999***********************************
4000 REM Choose Random Number
4005cJ=ABSRND
4007 REM Unpack Number
4010uFOR K=0 TO 3
4020 M?K=J%10
4030 J=J/10
4040 NEXT
4050 RETURN
4999***********************************
5000 REM Print Guess
5010gFOR K=0 TO 3
5020 P. $(H&15+#30)
5030 H=H/256; NEXT
5040 RETURN
5999********%**************************
6000 REM Your Turn
6040aPRINT "YOUR GUESS"
6045 INPUT J
6050 GOSUB u
6060 !N=G
6065 LINK LL2
6070 P.?B" BULLS, "?C" COWS"'
6075 IF!C<>#400 RETURN
6080 IF Z PRINT"...AND YOU WIN"'
_127_
6083 IF Z:1 PRINT" ABOUT TIME T00!"'
6085 Y=0
6090 RETURN
6999***********************************
7000 REM My Turn 7090bPRINT "MY GUESS: 7100 H=Q; GOSUB g 7110 PRINT ’ 7120 INPUT "REPLY" V 7140 RR(I)=(V/10)*256+V%10 7150 GG(I)=Q 7225 IF V<>40 GOSUB f; RETURN 7230 IF Y PRINT"...SO I WIN!"' 7235 Z=0 7240 RETURN 7999***********************************
9000zREM Find Bulls/Cows 9035 PRINT $#15 ;REM Turn off screen 9045 DIM P(-1) 9050[ 9055\ find bulls 6 cows for m:n 9060:LL2 LDA @0; LDX #13 ZERO L,B,C 9065:LL3 STA C,X; DEX; BPL LL3 9100 LDY @3 9105:LL0 9120 LDA M,Y 9130 CMP N,Y is bull? 9140 BNE LL4 no bull 9150 INC B count bull 9160 BPL LL1 no cows i 9165:LL4 9170 TAX not a bull 9180 INC L,X 9190 BEQ LL6 9200 BPL LL5 not a cow 9210:LL6 INC C 9220:LL5 LDX N,Y; DEC L,X 9225 BMI LL1; INC C 9260:LL1 DEY; BPL LLO again 9350 RTS 9360\ increment M 9370:LL7 SED; SEC; LDY @3 9380:LL9 LDA M,Y; ADC @#90 9390 BCS LL8; AND @#0F 9400:LL8 STA M,Y; DEY 9410 BPL LL9; RTS 9500] 9900 PRINT $#6 ;REM Turn Screen on 9910 RETURN
Description of Program:
_130_20-25 Declare arrays and vectors 50-60 Assemble machine code 1010 Computer chooses code 1020 Choose number for first guess 1040-1350 Main program loop 1050 Print turn number 110G If you have not finished – have a turn 1150 If I have not finished – my turn 1350 Carry on until we have both finished _128_ 1999 Lines to make listing more readable. 2000-3999 f: Find a guess which is compatible with all your replies to my previous guesses. 4000-4999 c: Choose a random number 4007-4050 u: Unpack J into byte vector M, one digit per byte. 5000-5040 g: Print guess in K as four digits. 6000-6090 a: Human's guess at machine's number; print score. 7000-7240 b: Machine's guess at human's code. 9000-991O z: Subroutine to assemble machine-code routines 9055-9350 Find score between numbers in byte vectors M and N; return in ?B and ?C. 9360-9500 Increment number in vector M, in decimal, one digit per byte.Variables:?B – Number of Bulls between vectors M and N ?C – Number of Cows between vectors M and N GG(1..10) – List of human's guesses H – Computer's number I – Turn number J – Human's guess as 4-digit decimal number K – Counter L – Vector to count occurrences of digits in numbers LL(0..10) – Labels in assembler routines LL2 – Entry point to routine to find score between 2 codes LL7 – Entry point to routine to increment M !M, !N – Code numbers to be compared P – Location counter Q – Computer's guess, compatible with human's previous replies. RR(1..10) – List of human's replies to guesses GG(1..10) Y – Zero if human has finished Z – Zero if computer has finished. Program size: 1982 bytes Additional storage: 152 bytes Machine-code: 223 bytes Total storage: 2357 bytesSample run:>RUN ( 1) YOUR GUESS?1122 0 BULLS, 0 COWS MY GUESS: 6338 REPLY?10 ( 2) YOUR GUESS?3344 0 BULLS, 0 COWS MY GUESS: 6400 REPLY?20 ( 3) YOUR GUESS?5566 0 BULLS, 0 COWS MY GUESS: 6411 REPLY?10 ( 4) YOUR GUESS?7788 1 BULLS, 1 COWS MY GUESS: 6502 REPLY?40 ...SO I WIN! ( 5) _129_ YOUR GUESS?