| Atom Nieuws jaargang 2000 nummer 1 |



|
pagina 10 |
Gevulde driehoeken
door Roland Leurs Dit is geen recept voor een nieuwe lekkernij, maar een betoog over het tekenen van een ingekleurde driehoek. Het tekenen van een gewone driehoek stelt in principe weinig voor: je tekent drie lijnen en klaar. Het wordt echter een stuk minder aangenaam als we deze driehoek ook nog willen inkleuren. Zoals bijvoorbeeld de BBC en Electron de mogelijkheid hebben om met PLOT85 een driehoek op het scherm weer te geven. Het eerste probleem begint al bij de vorm en de orientatie van de driehoek. We kennen rechthoekige driehoeken, gelijkbenige driehoeken, schots en scheve driehoeken enz.
door Roland Leurs Dit is geen recept voor een nieuwe lekkernij, maar een betoog over het tekenen van een ingekleurde driehoek. Het tekenen van een gewone driehoek stelt in principe weinig voor: je tekent drie lijnen en klaar. Het wordt echter een stuk minder aangenaam als we deze driehoek ook nog willen inkleuren. Zoals bijvoorbeeld de BBC en Electron de mogelijkheid hebben om met PLOT85 een driehoek op het scherm weer te geven. Het eerste probleem begint al bij de vorm en de orientatie van de driehoek. We kennen rechthoekige driehoeken, gelijkbenige driehoeken, schots en scheve driehoeken enz.

We kunnen het ons gemakkelijk maken,
zeker in de Atom, door een open driehoek te tekenen en deze
vervolgens met het PAINT statement van de GAGSROM te kleuren.
Ofschoon dit in de praktijk meestal voldoende werkt, kan het
voorkomen dat de driehoek niet helemaal ingekleurd wordt. Op
soortgelijke wijze werkt ook het XTRIANGLE statement van de
Atom-in-PC. De auteur was destijds niet slim genoeg om een goed
algoritme te zoeken of te bedenken.
Er zijn twee mogelijkheden om een
gevulde driehoek te tekenen. Beiden gaan uit van het Bressenham
algoritme voor het tekenen van een lijn. Leendert Bijnagte heeft daar
al eens zinnige woorden over geschreven, zoekt u maar eens op de
Atomware CD naar "Zullen we een lijntje trekken".
De eerste methode, waarvan ik alleen de
globale werking even schets, bevat het "in gedachten tekenen"
van diverse lijnstukken. Allereerst worden de drie hoekpunten
gesorteerd op y-co÷rdinaat. Stel we gaan uit van een driehoek
waarvan we de hoekpunten A, B en C noemen. Zie de figuur hieronder.
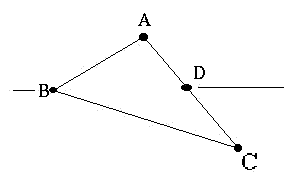
We bedenken een denkbeeldig vierde punt op de driehoek, punt D. Wat we dan kunnen doen is met Bressenham gelijktijdig twee lijnstukken berekenen vanaf punt A naar punt B en vanaf punt A naar punt D. We krijgen dan telkens twee paar co÷rdinaten. Tussen deze co÷rdinaten tekenen we dan een horizontale lijn. Dit doen we dus net zolang totdat we bij punt B aangekomen zijn.
Daarna beginnen we aan twee nieuwe lijnstukken, van punt B naar punt C en van punt D naar punt C.Hier gebruiken we dezelfde methode. We tekenen dus als het ware twee driehoeken waarvan de onderste resp. de bovenste lijnen horizontaal liggen. Het moeilijke van dit algoritme is het gelijktijdig berekenen van twee
lijnstukken en de daarbij behorende controles op eindpunten. Zeker
als we dat in assembler gaan doen. Het wordt nog ingewikkelder als we
dit algoritme willen uitbreiden om een ingekleurde polygoon te teken
met bijvoorbeeld 7 zijden.
Het tweede algoritme is wat
eenvoudiger. We gaan ook hier met Bressenham werken, maar nu telkens
voor ÚÚn lijnstuk tegelijk. Het idee erachter is om
twee arrays te definiŰren met zoveel elementen als er punten op
de y-as liggen. We hebben dan een linker en een rechter array; laten
we deze LLy en RRy noemen. We vullen alle elementen van de array LLy
met de grootste
waarde die voorkomt op de x-as en de array RRy vullen we met de
kleinste waarde die voorkomt op de x-as.
Als we de driehoek bovenaan
deze bladzijde weer als voorbeeld nemen hebben we dus twee arrays met
yc-ya elementen. LLy wordt gevuld met xc en RRy wordt gevuld met xb.
We gaan nu de punten
berekenen op het lijnstuk tussen de punten A en B. Voor elk punt
testen we of het array element LLy kleiner is dan de y co÷rdinaat
van het zojuist berekende punt. Als dat zo is nemen we deze
co÷rdinaat over in de linker array. Deze controle voeren we ook
uit op de RRy en indien de y co÷rdinaat groter is dan nemen we
deze ook over in de rechter array.
Het moeilijke van dit algoritme is het gelijktijdig berekenen van twee
lijnstukken en de daarbij behorende controles op eindpunten. Zeker
als we dat in assembler gaan doen. Het wordt nog ingewikkelder als we
dit algoritme willen uitbreiden om een ingekleurde polygoon te teken
met bijvoorbeeld 7 zijden.
Het tweede algoritme is wat
eenvoudiger. We gaan ook hier met Bressenham werken, maar nu telkens
voor ÚÚn lijnstuk tegelijk. Het idee erachter is om
twee arrays te definiŰren met zoveel elementen als er punten op
de y-as liggen. We hebben dan een linker en een rechter array; laten
we deze LLy en RRy noemen. We vullen alle elementen van de array LLy
met de grootste
waarde die voorkomt op de x-as en de array RRy vullen we met de
kleinste waarde die voorkomt op de x-as.
Als we de driehoek bovenaan
deze bladzijde weer als voorbeeld nemen hebben we dus twee arrays met
yc-ya elementen. LLy wordt gevuld met xc en RRy wordt gevuld met xb.
We gaan nu de punten
berekenen op het lijnstuk tussen de punten A en B. Voor elk punt
testen we of het array element LLy kleiner is dan de y co÷rdinaat
van het zojuist berekende punt. Als dat zo is nemen we deze
co÷rdinaat over in de linker array. Deze controle voeren we ook
uit op de RRy en indien de y co÷rdinaat groter is dan nemen we
deze ook over in de rechter array.
Ditzelfde herhalen we voor alle punten op dit lijnstuk en op de overige lijnstukken. Als dat gebeurd is hoeven we alleen nog maar met een eenvoudige lus de array te doorlopen en rechte lijnen te trekken tussen de punten LLy en RRy voor iedere y co÷rdinaat van de driehoek. Het voordeel van deze aanpak is dat het een behoorlijk stuk eenvoudiger is omdat we maar slechts aan ÚÚn lijnstuk gelijktijdig rekenen. Dit maakt het ook eenvoudiger om het algoritme toe te passen voor onze polygoon met 7 hoeken. Een nadeel is dat we veel meer (tijdelijk) geheugen nodig hebben voor het opslaan van de co÷rdinaten. In een clear-4 scherm kan dat oplopen tot twee arrays van 192 elementen. Wetende dat ieder element vier bytes beslaat, komen we uit op 2 * 192 * 4 = 1536 bytes. Uiteraard kunnen we dat nog terugbrengen door niet met een array te werken, maar door het rechtstreeks aanspreken van geheugenadressen met behulp van de ? operator. In dat geval hebben we slechts 2 * 192 = 384 bytes nodig. Laten we het laatste algoritme eens in basic bekijken: 10 PROGRAM DRIEHOEK
20 REM ROLAND LEURS, FEBRUARI 2000
30 ;
40 PROC TRIANGLE(A,B,C,D,E,F),I,V,W,X,Y
50 REM INITIALISEER LINKER EN RECHTER ARRAY
60 FOR I=0 TO 191
70 LL(I)=256; RR(I)=-1
80 NEXT I
90 REM BEREKEN VOOR DE DRIE LIJNSTUKKEN ALLE PUNTEN
100 FOR I=1 TO 3
110 IF I=1 THEN V=A;W=B;S=C;T=D
120 IF I=2 THEN V=C;W=D;S=E;T=F
130 IF I=3 THEN V=A;W=B;S=E;T=F
140 REM BEREKEN DE PUNTEN ADV BRESSENHAM ALGORITME
150 X=V;Y=W;K=S-V;M=ABS(K)
160 L=T-W;N=ABS(L)
170 IF M>=N THEN GOTO a
180 Q=(-1*N)/2
190f IF Y=T THEN GOTO c
200 IF X<=LL(Y) THEN LL(Y)=X
210 IF X>=RR(Y) THEN RR(Y)=X
220 Q=Q+M
230 XIF L<0 THEN Y=Y-1
240 ELSE Y=Y+1
250 IF Q<=0 THEN GOTO b
260 Q=Q-N
270 XIF K<0 THEN X=X-1
280 ELSE X=X+1
290b GOTO f
300a Q=M/2
310e IF X=S THEN GOTO c
320 IF X<=LL(Y) THEN LL(Y)=X
330 IF X>=RR(Y) THEN RR(Y)=X
340 Q=Q-N
350 XIF K<0 THEN X=X-1
360 ELSE X=X+1
370 IF Q>=0 THEN GOTO d
380 Q=Q+M
390 XIF L<0 THEN Y=Y-1
400 ELSE Y=Y+1
410d GOTO e
420c NEXT I
430 IF X<=LL(Y) THEN LL(Y)=X
440 IF X>=RR(Y) THEN RR(Y)=X
450 REM BEPAAL GROOTSTE EN KLEINSTE Y COORDINAAT
460 IF B<=D AND B<=F THEN W=B
470 IF D<=B AND D<=F THEN W=D
480 IF F<=B AND F<=D THEN W=F
490 IF B>=D AND B>=F THEN T=B
500 IF D>=B AND D>=F THEN T=D
510 IF F>=B AND F>=D THEN T=F
520 REM TEKEN DE HORIZONTALE LIJNEN DIE DE DRIEHOEK VORMEN
530 FOR I=W TO T
540 MOVE LL(I),I;DRAW RR(I),I
550 NEXT I
560 PEND
570 ;
580 REM DEMONSTRUCTIE
590 DIM LL(256),RR(256)
600 CLEAR 4
610 TRIANGLE(10,10,50,10,10,50)
620 TRIANGLE(10,100,10,150,150,10)
630 TRIANGLE(250,190,200,150,225,55)
640 TRIANGLE(100,96,160,96,130,190)
650 END
Met vriendelijke groeten uit een zonnig Born,
Roland Leurs.

We bedenken een denkbeeldig vierde punt op de driehoek, punt D. Wat we dan kunnen doen is met Bressenham gelijktijdig twee lijnstukken berekenen vanaf punt A naar punt B en vanaf punt A naar punt D. We krijgen dan telkens twee paar co÷rdinaten. Tussen deze co÷rdinaten tekenen we dan een horizontale lijn. Dit doen we dus net zolang totdat we bij punt B aangekomen zijn.
Daarna beginnen we aan twee nieuwe lijnstukken, van punt B naar punt C en van punt D naar punt C.Hier gebruiken we dezelfde methode. We tekenen dus als het ware twee driehoeken waarvan de onderste resp. de bovenste lijnen horizontaal liggen.
 Het moeilijke van dit algoritme is het gelijktijdig berekenen van twee
lijnstukken en de daarbij behorende controles op eindpunten. Zeker
als we dat in assembler gaan doen. Het wordt nog ingewikkelder als we
dit algoritme willen uitbreiden om een ingekleurde polygoon te teken
met bijvoorbeeld 7 zijden.
Het tweede algoritme is wat
eenvoudiger. We gaan ook hier met Bressenham werken, maar nu telkens
voor ÚÚn lijnstuk tegelijk. Het idee erachter is om
twee arrays te definiŰren met zoveel elementen als er punten op
de y-as liggen. We hebben dan een linker en een rechter array; laten
we deze LLy en RRy noemen. We vullen alle elementen van de array LLy
met de grootste
waarde die voorkomt op de x-as en de array RRy vullen we met de
kleinste waarde die voorkomt op de x-as.
Als we de driehoek bovenaan
deze bladzijde weer als voorbeeld nemen hebben we dus twee arrays met
yc-ya elementen. LLy wordt gevuld met xc en RRy wordt gevuld met xb.
We gaan nu de punten
berekenen op het lijnstuk tussen de punten A en B. Voor elk punt
testen we of het array element LLy kleiner is dan de y co÷rdinaat
van het zojuist berekende punt. Als dat zo is nemen we deze
co÷rdinaat over in de linker array. Deze controle voeren we ook
uit op de RRy en indien de y co÷rdinaat groter is dan nemen we
deze ook over in de rechter array.
Het moeilijke van dit algoritme is het gelijktijdig berekenen van twee
lijnstukken en de daarbij behorende controles op eindpunten. Zeker
als we dat in assembler gaan doen. Het wordt nog ingewikkelder als we
dit algoritme willen uitbreiden om een ingekleurde polygoon te teken
met bijvoorbeeld 7 zijden.
Het tweede algoritme is wat
eenvoudiger. We gaan ook hier met Bressenham werken, maar nu telkens
voor ÚÚn lijnstuk tegelijk. Het idee erachter is om
twee arrays te definiŰren met zoveel elementen als er punten op
de y-as liggen. We hebben dan een linker en een rechter array; laten
we deze LLy en RRy noemen. We vullen alle elementen van de array LLy
met de grootste
waarde die voorkomt op de x-as en de array RRy vullen we met de
kleinste waarde die voorkomt op de x-as.
Als we de driehoek bovenaan
deze bladzijde weer als voorbeeld nemen hebben we dus twee arrays met
yc-ya elementen. LLy wordt gevuld met xc en RRy wordt gevuld met xb.
We gaan nu de punten
berekenen op het lijnstuk tussen de punten A en B. Voor elk punt
testen we of het array element LLy kleiner is dan de y co÷rdinaat
van het zojuist berekende punt. Als dat zo is nemen we deze
co÷rdinaat over in de linker array. Deze controle voeren we ook
uit op de RRy en indien de y co÷rdinaat groter is dan nemen we
deze ook over in de rechter array. Ditzelfde herhalen we voor alle punten op dit lijnstuk en op de overige lijnstukken. Als dat gebeurd is hoeven we alleen nog maar met een eenvoudige lus de array te doorlopen en rechte lijnen te trekken tussen de punten LLy en RRy voor iedere y co÷rdinaat van de driehoek. Het voordeel van deze aanpak is dat het een behoorlijk stuk eenvoudiger is omdat we maar slechts aan ÚÚn lijnstuk gelijktijdig rekenen. Dit maakt het ook eenvoudiger om het algoritme toe te passen voor onze polygoon met 7 hoeken. Een nadeel is dat we veel meer (tijdelijk) geheugen nodig hebben voor het opslaan van de co÷rdinaten. In een clear-4 scherm kan dat oplopen tot twee arrays van 192 elementen. Wetende dat ieder element vier bytes beslaat, komen we uit op 2 * 192 * 4 = 1536 bytes. Uiteraard kunnen we dat nog terugbrengen door niet met een array te werken, maar door het rechtstreeks aanspreken van geheugenadressen met behulp van de ? operator. In dat geval hebben we slechts 2 * 192 = 384 bytes nodig. Laten we het laatste algoritme eens in basic bekijken: 10 PROGRAM DRIEHOEK
20 REM ROLAND LEURS, FEBRUARI 2000
30 ;
40 PROC TRIANGLE(A,B,C,D,E,F),I,V,W,X,Y
50 REM INITIALISEER LINKER EN RECHTER ARRAY
60 FOR I=0 TO 191
70 LL(I)=256; RR(I)=-1
80 NEXT I
90 REM BEREKEN VOOR DE DRIE LIJNSTUKKEN ALLE PUNTEN
100 FOR I=1 TO 3
110 IF I=1 THEN V=A;W=B;S=C;T=D
120 IF I=2 THEN V=C;W=D;S=E;T=F
130 IF I=3 THEN V=A;W=B;S=E;T=F
140 REM BEREKEN DE PUNTEN ADV BRESSENHAM ALGORITME
150 X=V;Y=W;K=S-V;M=ABS(K)
160 L=T-W;N=ABS(L)
170 IF M>=N THEN GOTO a
180 Q=(-1*N)/2
190f IF Y=T THEN GOTO c
200 IF X<=LL(Y) THEN LL(Y)=X
210 IF X>=RR(Y) THEN RR(Y)=X
220 Q=Q+M
230 XIF L<0 THEN Y=Y-1
240 ELSE Y=Y+1
250 IF Q<=0 THEN GOTO b
260 Q=Q-N
270 XIF K<0 THEN X=X-1
280 ELSE X=X+1
290b GOTO f
300a Q=M/2
310e IF X=S THEN GOTO c
320 IF X<=LL(Y) THEN LL(Y)=X
330 IF X>=RR(Y) THEN RR(Y)=X
340 Q=Q-N
350 XIF K<0 THEN X=X-1
360 ELSE X=X+1
370 IF Q>=0 THEN GOTO d
380 Q=Q+M
390 XIF L<0 THEN Y=Y-1
400 ELSE Y=Y+1
410d GOTO e
420c NEXT I
430 IF X<=LL(Y) THEN LL(Y)=X
440 IF X>=RR(Y) THEN RR(Y)=X
450 REM BEPAAL GROOTSTE EN KLEINSTE Y COORDINAAT
460 IF B<=D AND B<=F THEN W=B
470 IF D<=B AND D<=F THEN W=D
480 IF F<=B AND F<=D THEN W=F
490 IF B>=D AND B>=F THEN T=B
500 IF D>=B AND D>=F THEN T=D
510 IF F>=B AND F>=D THEN T=F
520 REM TEKEN DE HORIZONTALE LIJNEN DIE DE DRIEHOEK VORMEN
530 FOR I=W TO T
540 MOVE LL(I),I;DRAW RR(I),I
550 NEXT I
560 PEND
570 ;
580 REM DEMONSTRUCTIE
590 DIM LL(256),RR(256)
600 CLEAR 4
610 TRIANGLE(10,10,50,10,10,50)
620 TRIANGLE(10,100,10,150,150,10)
630 TRIANGLE(250,190,200,150,225,55)
640 TRIANGLE(100,96,160,96,130,190)
650 END
 | Bovenstaand
voorbeeld is grotendeels gebaseerd op het Bressenham algoritme om
lijnen te trekken. Leendert B. heeft daar al wijze woorden over
geschreven in Atom Nieuws 1994 nr 3 p.51. Het
programma is geschreven voor een standaard Atom, het draait ook
zonder aanpassingen op de Atom-in-PC kaart en uiteraard in de Atom
emulatoren. P-Charme is wel noodzakelijk omdat er gebruik gemaakt
wordt van een procedure en XIF/ELSE statements. aardige programmeeroefening mag u zelf de aanpassingen maken om een gevulde polygoon te tekenen. We lezen het resultaat wel in Atom Nieuws :-) |
Roland Leurs.


